Selection Sort¶
Use the visualization below to figure out how selection sort works.
Visualization¶
Or you can check out bubble (and other sorting algorithms) using this sorting visualizer. Just be careful with selection sort, as this external visualizer selects the smallest value instead of the largest. Although the logic is the same, we’ll implement this by selecting the largest value (as shown in the visualizer above).
Algorithm¶
The selection sort improves on the bubble sort by making only one exchange for every pass through the list. In order to do this, a selection sort looks for the largest value as it makes a pass and, after completing the pass, places it in the proper location. As with a bubble sort, after the first pass, the largest item is in the correct place. After the second pass, the next largest is in place. This process continues and requires \(n-1\) passes to sort \(n\) items, since the final item must be in place after the \((n-1)\) st pass.
The following image shows the entire sorting process. On each pass, the largest remaining item is selected and then placed in its proper location. The first pass places 93, the second pass places 77, the third places 55, and so on.
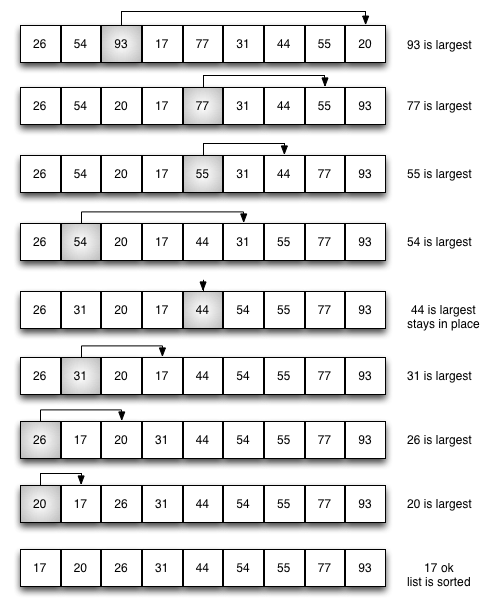
Selection Sort: Complete¶
Pencil and Paper Practice¶
On a piece of paper, show the iterations done by selection sort for the list {5,15,3,8,9,1,20,7}
Code the Algorithm¶
See if you can implement an algorithm for selection sort. You may want to begin by adapting the bubble sort code you created.